組み合わせ回路では、エンコーダ、マルチプレクサ、デコーダ、デマルチプレクサを設計するためにさまざまな論理ゲートが使用されます。これらの回路には、この回路の出力が主にいつでも入力端子にあるレベルに依存するようないくつかの特性があります。この回路にはメモリが含まれていません。入力の初期の状態は、この回路の現在の状態に影響を与えません。組み合わせ回路の入力と出力は「n」ではありません。入力の数と「m」番号出力の。組み合わせ回路には、半加算器と全加算器、減算器、エンコーダー、デコーダー、マルチプレクサー、およびデマルチプレクサーがあります。この記事では、半加算器と全加算器の概要と、真理値表の操作について説明します。

加算器とは何ですか？

加算器はデジタル論理回路数字の加算に広く使用されている電子機器で。多くのコンピュータやその他のタイプのプロセッサでは、加算器はアドレスや関連アクティビティの計算、ALUのテーブルインデックスの計算に使用され、プロセッサの他の部分でも使用されます。これらは、excess-3や2進化10進数などの多くの数値表現用に作成できます。加算器は基本的に、半加算器と全加算器の2つのタイプに分類されます。

半加算器と全加算器回路とは何ですか？

半加算回路には、AとBの2つの入力があり、2つの入力桁を加算して、キャリーと合計を生成します。全加算回路には、AとCの3つの入力があり、3つの入力番号を加算して、キャリーと合計を生成します。この記事では、半加算器の目的について詳しく説明します。 そして 表形式の全加算器、さらには回路図でも。加算器の主で重要な目的は加算であることはすでに述べました。以下は詳細です 半加算器と全加算器の理論。

基本的な半加算器と全加算器

半加算器

したがって、半加算器のシナリオでは、入力ビットが加数および加数と呼ばれる2桁の2進数が加算され、結果は2つの出力になります。1つは合計で、もう1つはキャリーです。合計演算を実行するには、XORを両方の入力に適用し、ANDゲートを両方の入力に適用してキャリーを生成します。

HA機能図

一方、全加算回路では、3つの1ビット数を加算します。3ビットのうち2つはオペランドと呼ばれ、もう1つはビットキャリーインと呼ばれます。生成される出力は2ビット出力であり、これらを参照できます。出力キャリーと合計としてに。

半加算器を使用すると、論理ゲートを使用して簡単な加算を設計できます。

2つのシングルビットを追加する例を見てみましょう。

2ビット 半加算器の真理値表 以下のとおりです。

半加算器の真理値表

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

これらは、可能な限り最小のシングルビットの組み合わせです。ただし、1 + 1の結果は10であり、合計結果は2ビット出力として書き直す必要があります。したがって、方程式は次のように書くことができます。

0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10

“ネットワークインターフェイスカード（nic）の冗長性の2つのモードは次のうちどれですか？ ”

「10」の出力「1」はキャリーアウトです。「SUM」は通常の出力であり、「CARRY」はキャリーアウトです。

これで、出力「SUM」のXORゲートと「キャリー」のANDゲートを使用して、1ビット加算器を簡単に実装できることが明らかになりました。

たとえば、2つの8ビットバイトを加算する必要がある場合は、全加算器の論理回路を使用して実装できます。半加算器は、1桁の2進数を加算する場合に便利です。

2進数の加算器を開発する方法は、真理値表を作成してそれを減らすことです。 3進数の加算器を作成する場合は、半加算器の加算演算を2回実行します。同様に、4桁の加算器を作成する場合は、もう一度操作を行います。この理論から、実装は簡単であることが明らかでしたが、開発には時間がかかります。

最も単純な式は、排他的論理和関数を使用します。

Sum = A XOR B

キャリー= A AND B

HA論理図

また、基本的なAND、OR、およびNOTに関する同等の式は次のとおりです。

SUM = A.B + A.B ’

半加算器のVHDLコード

エンティティhaは

ポート（a：STD_LOGIC内
b：STD_LOGIC内
sha：アウトSTD_LOGIC
cha：アウトSTD_LOGIC）
終わりは

上記の回路のアーキテクチャの動作は

ベギン
しゃ<= a xor b
番号<= a and b
行動を終了する

半加算器IC番号

半加算器の実装は、SN74HC08（7408）およびSN74HC86（7486）を含む74HCxxシリーズのような高速CMOSデジタルロジック集積回路を介して行うことができます。

半加算器の制限

半加算器のようにこれらのバイナリ加算器を呼び出す主な理由は、前のビットを使用してキャリービットを含める範囲がないためです。したがって、これは、特に数ビットの加算を伴うリアルタイムの状況で、バイナリ加算器のように使用されたHAの主な制限です。したがって、この制限は全加算器を使用することで克服できます。

全加算器

この加算器は、半加算器と比較すると実装が困難です。

全加算器の機能図

半加算器と全加算器の違いは、全加算器には3つの入力と2つの出力があるのに対し、半加算器には2つの入力と2つの出力しかないことです。最初の2つの入力はAとBで、3番目の入力はC-INとしての入力キャリーです。全加算器ロジックを設計するときは、それらの8つをつなぎ合わせてバイト幅の加算器を作成し、キャリービットを1つの加算器から次の加算器にカスケードします。

FA真理値表

出力キャリーはC-OUTとして指定され、通常の出力は「SUM」であるSとして表されます。

上記で 全加算器の真理値表 、全加算回路の実装は簡単に理解できます。 SUM「S」は2つのステップで生成されます。

提供された入力「A」と「B」をXORすることによって
次に、A XORBの結果がC-INとXORされます。

これによりSUMが生成され、C-OUTは3つの入力のいずれかがHIGHの場合にのみ真になり、C-OUTはHIGHになります。したがって、2つの半加算回路を使用して全加算回路を実装できます。最初に、半加算器を使用してAとBを加算して部分和を生成し、後半の加算器ロジックを使用して、前半加算器によって生成された和にC-INを加算して、最終的なS出力を取得できます。

半加算ロジックのいずれかがキャリーを生成する場合、出力キャリーがあります。したがって、C-OUTは半加算器のキャリー出力のOR関数になります。以下に示す全加算器回路の実装を見てください。

全加算器の論理図

上記の全加算器ロジックを使用すると、より大きな論理図の実装が可能です。ほとんどの場合、操作を表すために、より単純な記号が使用されます。以下に示すのは、1ビット全加算器のより単純な回路図です。

このタイプのシンボルを使用すると、2ビットを加算して、次に低い桁からキャリーを取得し、次に高い桁にキャリーを送信できます。コンピューターでは、マルチビット演算の場合、各ビットは全加算器で表され、同時に加算される必要があります。したがって、2つの8ビット数を加算するには、4ビットブロックの2つをカスケードすることによって形成できる8つの全加算器が必要になります。

K-Mapを使用した半加算器と全加算器

半加算器の合計出力とキャリー出力でさえ、カルノー図（K-map）の方法で取得できます。ザ・ 半加算器と全加算器のブール式 K-mapから取得できます。したがって、これらの加算器のKマップについては以下で説明します。

半加算器のKマップは

HAKマップ

全加算器のK-Mapは

FAKマップ

SUMとキャリーの論理式

合計（S）の論理式は、表に記載されている入力に基づいて決定できます。

= A’B’Cin + A’B CCin ’+ A B’Cin’ + AB Cin
= Cin（A’B ’+ AB）+ Cin’（A’B + A B ’）
= Cin EX-OR（A EX-OR B）
=（1,2,4,7）

キャリー（Cout）の論理式は、表に記載されている入力に基づいて決定できます。

= A’B Cin + AB’Cin + AB Cin ’+ ABCin
= AB + BCin + ACin
=（3、5、6、7）

上記の真理値表を使用すると、結果を取得でき、手順は次のとおりです。

組み合わせ回路は、回路内のさまざまなゲートを組み合わせて、エンコーダ、デコーダ、マルチプレクサとデマルチプレクサ。組み合わせ回路の特徴は次のとおりです。

任意の時点での出力は、入力端子に存在するレベルのみに基づいています。
メモリを使用しません。以前の入力状態は、回路の現在の状態に影響を与えません。
任意の数の入力とm個の出力を持つことができます。

VHDLコーディング

全加算器のVHDLコーディング 以下のものが含まれます。

エンティティfull_addは

ポート（：STD_LOGIC内
b：STD_LOGIC内
cin：STD_LOGIC内
合計：STD_LOGICから
cout：out STD_LOGIC）
full_addを終了します

full_addのアーキテクチャの動作は

コンポーネントhaは
ポート（：STD_LOGIC内
b：STD_LOGIC内
sha：アウトSTD_LOGIC
cha：アウトSTD_LOGIC）
エンドコンポーネント
信号s_s、c1、c2：STD_LOGIC
ベギン
HA1：haポートマップ（a、b、s_s、c1）
HA2：haポートマップ（s_s、cin、sum、c2）
費用<=c1 or c2
行動を終了する

ザ・ 半加算器と全加算器の違い つまり、半加算器は結果を生成し、全加算器は半加算器を使用して他の結果を生成します。同様に、全加算器は2つの半加算器ですが、全加算器は、算術回路を作成するために使用する実際のブロックです。

キャリー先見加算器

リップルキャリー加算器回路の概念では、加算に必要なビットがすぐに利用可能になります。一方、すべての加算器セクションは、前の加算器ブロックからのキャリーの到着のための時間を保持する必要があります。このため、回路の各セクションが入力の到着を待機するため、SUMとCARRYの生成に時間がかかります。

たとえば、n番目のブロックに出力を配信するには、（n-1）番目のブロックから入力を受信する必要があります。そして、この遅延は、対応して伝搬遅延と呼ばれます。

リップルキャリー加算器の遅延を克服するために、キャリールックアヘッド加算器が導入されました。ここでは、複雑なハードウェアを使用することで、伝搬遅延を最小限に抑えることができます。次の図は、全加算器を使用したキャリー先見加算器を示しています。

全加算器を使用して先見を実行する

真理値表と対応する出力方程式は次のとおりです。

に	B	C	C + 1	状態
0	0	0	0	キャリーなし生む
0	0	1	0
0	1	0	0
0	1	1	1	キャリーなし伝播する
1	0	0	0
1	0	1	1
1	1	0	1	運ぶ生む
1	1	1	1	運ぶ生む

キャリー伝播方程式はPi = Ai XOR Biであり、キャリー生成はGi = Ai * Biです。これらの方程式を使用すると、合計方程式とキャリー方程式は次のように表すことができます。

“光センサーはどのように機能しますか ”

SUM = Pi XOR Ci

Ci + 1 = Gi + Pi * Ci

Giは、入力キャリーを考慮せずに、入力AiとBiの両方が1の場合にのみキャリーを提供します。 Piは、CiからCi +1へのキャリー伝搬に関連しています。

半加算器と全加算器の違い

ザ・ 半加算器と全加算器テーブルの違い 以下に示します。

半加算器	全加算器
半加算器（HA）は組み合わせ論理回路であり、この回路は2つの1ビット桁を加算するために使用されます。	全加算器（FA）は組み合わせ回路であり、この回路は3つの1ビット桁を加算するために使用されます。
HAでは、前の加算からキャリーが生成されると、次のステップに加算することはできません。	FAでは、前の加算からキャリーが生成されると、次のステップに追加できます。
半加算器には、ANDゲートとEX-ORゲートのような2つの論理ゲートが含まれています。	全加算器には、2つのEX-ORゲート、2つのORゲート、および2つのANDゲートが含まれます。
半加算器の入力ビットは、A、Bのように2つです。	全加算器の入力ビットは、A、B、C-inのような3つです。
半加算器の合計とキャリーの式は S =a⊕bC= a * b	全加算器の論理式は S =a⊕b⊕CinCout=（a * b）+（Cin *（a⊕b））。
HAは、コンピューター、電卓、デジタル測定に使用されるデバイスなどで使用されます。	FAは、デジタルプロセッサ、マルチビット加算などで使用されます。

ザ・ 半加算器と全加算器の主な違い 以下で説明します。

半加算器は2つのバイナリ入力を加算して合計とキャリーを生成しますが、全加算器は3つのバイナリ入力を加算して合計とキャリーを生成するために使用されます。半加算器と全加算器の両方のハードウェアアーキテクチャは同じではありません。
HAとFAを区別する主な機能は、HAでは、最後の加算キャリーを入力のように考慮するような取引がないことです。ただし、FAは、最後の加算のキャリービットを考慮するためにCinのような特定の入力列を見つけます。
2つの加算器は、その構造のために回路で使用されるコンポーネントに基づいて違いを示します。半加算器（HA）は、ANDとEX-ORのような2つの論理ゲートの組み合わせで設計されていますが、FAは、3つのAND、2つのXORと1つのORゲートの組み合わせで設計されています。
基本的に、HAは1ビットの2〜2入力で動作しますが、FAは1ビットの3入力で動作します。半加算器は、加算を評価するためにさまざまな電子デバイスで使用されますが、全加算器は、長いビットを加算するためにデジタルプロセッサで使用されます。
これら2つの加算器の類似点は、HAとFAの両方が組み合わせデジタル回路であるため、順序回路などのメモリ要素を使用しないことです。これらの回路は、2進数の加算を提供する算術演算に不可欠です。

半加算器を使用した全加算器の実装

FAの実装は、論理的に接続された2つの半加算器を介して実行できます。このブロック図を以下に示します。これは、2つの半加算器を使用したFAの接続を示しています。
以前の計算からの合計とキャリーの方程式は次のとおりです。

S = A'B'Cin + A'BC 'in + ABCin

Cout = AB + ACin + BCin

和の方程式は次のように書くことができます。

Cin（A’B ‘+ AB）+ C‘in（A‘B + A B’）

したがって、Sum = Cin EX-OR（A EX-OR B）

Cin（A EX-OR B）+ C’in（A EX-OR B）

= Cin EX-OR（A EX-OR B）

Coutは次のように書くことができます。

COUT = AB + ACin + BCin。

COUT = AB + +失望BCIN（A + A）

= ABCin + AB + ACin + A’B Cin

= AB（1 + Cin）+ ACin + A’B Cin

= A B + ACin + A’B Cin

= AB + ACin（B + B ’）+ A’B Cin

= ABCin + AB + A’B Cin + A’B Cin

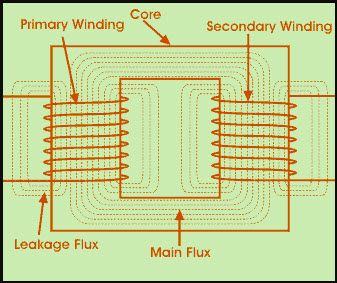
“電源トランスとは ”

= AB（Cin + 1）+ A B Cin + A’B Cin

= AB + AB’Cin + A’B Cin

= AB + Cin（AB ’+ A’B）

したがって、COUT = AB + Cin（A EX-OR B）

上記の2つの合計とキャリーの式に応じて、FA回路は2つのHAとORゲートを使用して実装できます。 2つの半加算器を備えた全加算器の回路図を上に示します。

2つの半加算器を使用した全加算器

NANDゲートを使用した全加算器の設計

NANDゲートは、あらゆる種類の論理設計を実行するために使用されるユニバーサルゲートの一種です。 NANDゲート図を使用したFA回路を以下に示します。

NANDゲートを使用したFA

FAは簡単な1ビット加算器であり、nビットの加算を実行したい場合は、nはありません。カスケード接続形式では、1ビットのFAを使用する必要があります。

利点

ザ・ 半加算器と全加算器の利点 以下のものが含まれます。

半加算器の主な目的は、2つのシングルビット数を加算することです。
全加算器は、前の加算の結果であるキャリービットを加算する機能を保持します
全加算器を使用すると、加算器、マルチプレクサなどの重要な回路を実装できます。
全加算器回路は最小限の電力を消費します
半加算器に対する全加算器の利点は、半加算器が主に2つの1ビット数を加算するために使用されるため、全加算器を使用して半加算器の欠点を克服することです。半加算器はキャリービットを追加しないため、この全加算器を克服するために採用されています。全加算器では、3ビットの加算を行うことができ、2つの出力を生成します。
加算器の設計は簡単で、1ビットの加算が簡単に理解できるように基本的な構成要素です。
この加算器は、インバーターを追加することで半減算器に変換できます。
全加算器を使用することにより、高出力を得ることができます。
高速
供給電圧スケーリングに非常に強い

短所

ザ・ 半加算器と全加算器の欠点 以下のものが含まれます。

また、半加算器は持ち運び前に使用できないため、マルチビット加算のカスケードには適用できません。
この欠点を克服するには、FAが3つの1ビットを追加する必要があります。
FAをRA（リップル加算器）のようなチェーンの形で使用すると、出力の駆動能力が低下する可能性があります。

アプリケーション

半加算器と全加算器のアプリケーションは次のとおりです。

バイナリビットの加算は、加算器を使用しているため、コンピュータ内でALUを使用して半加算器で実行できます。
半加算器の組み合わせは、全加算器回路の設計に使用できます。
半加算器は、計算機で使用され、アドレスとテーブルを測定します。
これらの回路は、デジタル回路内のさまざまなアプリケーションを処理するために使用されます。将来的には、デジタルエレクトロニクスにおいて重要な役割を果たします。
FA回路は、リップルキャリー加算器などの多くの大規模回路の要素として使用されます。この加算器は、ビット数を同時に加算します。
FAは算術論理演算装置（ALU）で使用されます
FAは、GPU（グラフィックスプロセッシングユニット）などのグラフィックス関連アプリケーションで使用されます。
これらは、キャリーアウト乗算を実行するための乗算回路で使用されます。
コンピュータでは、メモリアドレスを生成し、後続の命令に対するプログラムの対位法を構築するために、全加算器を使用して算術論理演算装置が使用されます。

したがって、2つの2進数の加算が行われるときはいつでも、数字は最初に最小ビットで加算されます。このプロセスは、2つの1ビット数を加算できる最も単純なn / wであるため、半加算器を介して実行できます。この加算器の入力は2進数ですが、出力は合計（S）とキャリー（C）です。

HAは以前のクラスのキャリー番号を追加できないため、桁数が含まれている場合は常に、HAネットワークを使用して最小桁を接続するだけです。全加算器は、すべてのデジタル演算デバイスのベースとして定義できます。これは、3つの1桁の数字を追加するために使用されます。この加算器には、A、B、Cinなどの3つの入力が含まれていますが、出力はSumとCoutです。