基本的な ネットワーク定理 ネットワーク分析で使用されるは、テブナン、重ね合わせ、ノートン、置換、最大電力伝達、相反性などのさまざまなタイプで利用できます & ミルマンの定理 .すべての定理には、独自の適用分野があります。したがって、これらの定理は異なる回路で繰り返し使用できるため、各ネットワーク定理を理解することは非常に重要です。これらの定理は、特定の条件で複雑なネットワーク回路を解決するのに役立ちます。この記事では、ネットワーク定理のタイプの 1 つについて説明します。 置換定理 – 例。
置換定理とは何ですか?
置換定理ステートメントは次のとおりです。ブランチ全体の電流またはネットワーク内のブランチ全体の電圧がわかっている場合はいつでも、そのブランチ全体で同様の電圧と電流を生成するさまざまな要素の組み合わせによってブランチを変更できます。つまり、次のように定義できます。熱電圧と電流は、ブランチの同等性のために同一でなければなりません。
置換定理の概念は、主にある要素を別の要素に置換することに依存します。この定理は、他のいくつかの定理を証明するのにも非常に役立ちます。ただし、この定理は、直列でも並列でも接続されていない上記の 2 つのソースを含む定理を解くには適用できません。
置換定理の説明
代入定理を解くために必要な手順は、主に次のとおりです。
ステップ1: まず、すべてのネットワーク要素の電圧と電流を見つける必要があります。一般に、電圧と電流はオームの法則を使用して計算できます。 キルヒョフの法則 KVL、または KCL のように。
ステップ2: 電圧源/抵抗や電流源などの別の要素を介して削除したい必要な分岐を選択します。
ステップ3: 電圧と電流が変化しないという条件で、置換された要素の正しい値を見つけます。
Step4: すべての要素の電流と電圧を計算するだけで新しい回路をチェックし、元のネットワークで評価します。
置換定理の回路図
次の回路図を使用して、置換定理を簡単に理解しましょう。置換定理は、単一の要素を別の同等の要素に置き換えることです。ネットワーク内のいずれかの要素が電流源または電圧源に置き換えられた場合、要素全体または要素全体の電流と電圧は以前のネットワークのように変化しません。
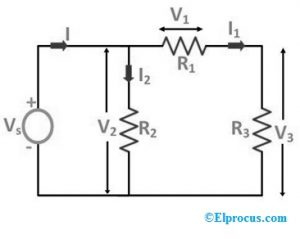
R1、R2、R3 などのさまざまな抵抗は、電圧源の両端に単純に接続されています。回路全体を流れる電流「I」の流れは I1 と I2 に分離され、「I1」は「R1」抵抗全体に供給され、「I2」は回路に示すように R2 抵抗全体に流れます。ここで、抵抗R1、R2、およびR3の両端の電圧降下は、対応してV1、V2、およびV3です。
ここで、次の回路図に示すように、「R3」抵抗を「V3」電圧源に置き換えると:
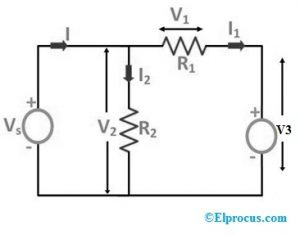
次の回路図では、「R3」抵抗は、その要素「I1」を流れる電流に置き換えられています。
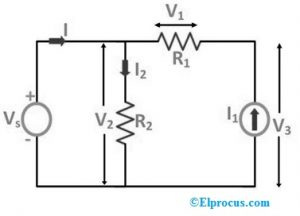
上記の2つのケースから、要素が電流源または電圧源に置き換えられた場合、回路の初期条件は変化しません。つまり、抵抗全体の電圧供給と抵抗全体の電流供給は、それらが他のものに置き換えられても変化しません。ソース。
問題例
代入定理の例の問題を以下で説明します。
例1:
次の回路を置換定理で解いて、すべての抵抗器内の電圧と電流を計算します。
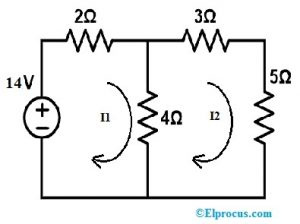
ステップ1:
まず、上記の回路の loop1 に KVL を適用します。
14 = 6I1 – 4I2 ….(1)
上記回路の loop2 に KVL を適用
0 = 12I2 – 4I1
12 I2 = 4I1 => I1 = 3I2…….(2)
この式 2 を上記の式 1 に代入します。
14 = 6(3I2) - 4I2
14 = 18I2 – 4I2 =>14I2 => 1A
I2 = 1A
上式-(2)より
I1 = 3I2
I2 = 1Aであることがわかっています
I1 = 3A
ステップ2:
このステップでは、loop1 ブランチを削除して単一のループを作成する必要があります。
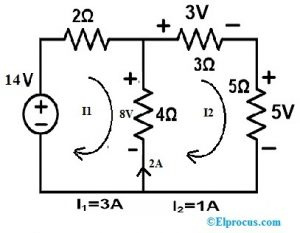
ステップ3:
4Ω抵抗の代わりに電流源/電圧源を配置できます。ここで、電流源を使用します。
回路の loop2 を流れる電流は 1A です。そこで、分岐を 1A の電流源に置き換えます。その結果、残りの回路は以下のようになります。
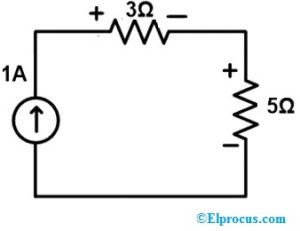
ステップ4:
このステップでは、すべての要素の電圧と電流を確認する必要があります。上記の回路は、単一のループ、すなわち電流源を含む。したがって、ループ全体に流れる電流の値は、電流源の値に似ています。
ここで、電流源の値は 1A です。そのため、3Ω と 5Ω の抵抗分岐を流れる電流は 1A で、元のネットワークと同様です。
を使用することにより、 オームの法則 、3Ω抵抗の両端の電圧値を見つけます
V = IS
V = 私 × R
V = 1 x 3 => 3V。
同様に、オームの法則を使用して、5Ω 抵抗の両端の電圧値を見つける必要があります。
V = IS
V = 私 × 5
V = 1 x 5 => 5V。
したがって、電流と電圧は元のネットワークに似ています。したがって、これがこの定理の仕組みです。
ここで、ステップ 3 で電流源の代わりに電圧源を選択するとします。したがって、この条件では、電圧源の値は 4Ω 抵抗分岐の値に似ています。
元のネットワーク内の 4Ω 抵抗ブランチ全体の電流の流れは次のとおりです。
I1 – I2 => 3 – 1 => 2A
オームの法則によると、
4Ω 抵抗の電圧は V = 2 x 4 = 8V
したがって、電圧源をネットワーク内の 8V に接続する必要があります。残りの回路を下の図に示します。
V = 2 × 4 = 8 V
したがって、8V 電圧源をネットワークに接続する必要があり、残りの回路は下の図のようになります。
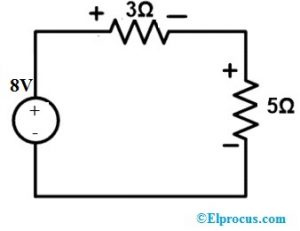
上記のループに KVL を適用して、電圧と電流を確認します。
8 = 3I + 5I => 8I
私=1A。
オームの法則を使用すると、抵抗 3Ω の両端の電圧は次のように計算できます。
V = 1 × 3 => 3V
同様に、抵抗器5Ωの両端の電圧は次のとおりです。
V= 1 × 5 => 5V
したがって、電圧と電流は交換後、元のネットワークと同じです。
例 2:
置換定理を適用するために次の回路を考えてみましょう。
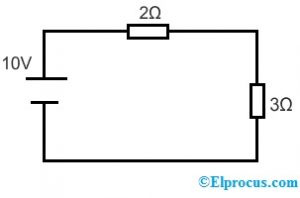
分圧定規によると、2Ωと3Ωの抵抗器の両端の電圧は次のとおりです。
3Ω抵抗の電圧は
V = 10×3/3+2 = 6V
2Ω抵抗の電圧は
V=10×2/3+2=4V
回路全体の電流の流れは、I = 10/3+2 = 2A として計算されます。
上記の回路で、3Ω抵抗の代わりに6V電圧源を代用すると、回路は次のようになります。
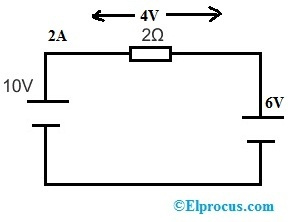
オームの法則に基づいて、2Ω 抵抗の両端の電圧と回路全体の電流の流れは次のようになります。
V = 10-6 => 4V
私 = 10-6/2 = 2A
3Ωの抵抗の代わりに2Aの電流源を代用すると、回路は次のようになります。
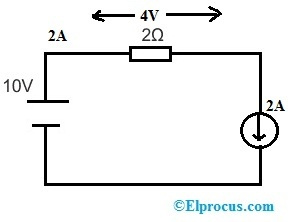
2Ω 抵抗の両端の電圧は V = 10 – 3* 2 => 4 V & 「2A」電流源の両端の電圧は V = 10 – 4 => 6 V. したがって、2Ω 抵抗の両端の電圧 & 回路全体の電流は変化しません。
利点
の 置換定理の利点 以下のものが含まれます。
- この定理の概念は、主に単一の要素を別の要素から置き換えることに依存しています。
- この定理は、回路の動作に関する直感を提供し、他のさまざまなネットワーク定理の検証にも役立ちます。
- この定理を使用する利点は、この定理が交点に対応する X や Y などの変数に正しい値を提供することです。
制限事項
の 置換定理の限界 以下のものが含まれます。
- この定理は、直列/並列に含まれない少なくとも 2 つ以上のソースを含むネットワークを解くためには使用できません。
- この定理では、素子を交換しても回路の挙動は変わらないはずです。
アプリケーション
の 置換定理の応用 以下のものが含まれます。
- 代入定理は、他の多くの定理を証明するために使用されます。
- この定理は、数学の連立方程式を解くのに役立ちます。
- この定理は、回路の 1 つの要素をもう 1 つの要素に置き換えます。
- この定理は、依存ソースを持つ回路を分析するために使用されます。
置換定理が適用されない回路は?
上記の2つのソースが並列または直列に接続されている回路では、この置換定理は適用されません。
なぜ補償定理は置換と呼ばれるのですか?
補償と置換の両方の定理は、手順と還元の点で同じです。したがって、この定理はアンテナにも適用でき、置換定理とも呼ばれます。
置換定理をどのように使用しますか?
この定理は、ネットワーク全体の電圧と電流を気にすることなく、ネットワーク内の任意の分岐を別の分岐に置き換えることで使用できます。したがって、この定理は線形回路と非線形回路の両方で使用されます。
代替物件とは?
置換プロパティは、変数 'a' が別の変数 'b' と等しい場合、任意の式または方程式で 'b' の代わりに 'a' を置き換えることができ、' の代わりに 'b' を置き換えることができることを示しています。任意の式または方程式の a'。
したがって、これはすべてについてです 置換の概要 定理 – 回路例。ここであなたに質問です。補償定理とは何ですか?