この記事では、標準的な工学式と説明を通じて、また線形1階微分方程式を適用して問題セットの例を解くことにより、オームの法則とキルヒホッフの法則を理解しようとします。

電気回路とは

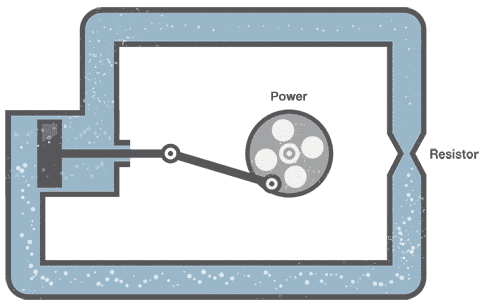
最も単純な電気回路は、一般に、バッテリーやDC発電機などからのエネルギー源または起電力入力と、このエネルギーを消費する抵抗性負荷、たとえば電球を備えた直列回路の形式です。下の図：

図を参照すると、スイッチが閉じているとき、電流私抵抗器を通過し、抵抗器の両端に電圧が発生します。つまり、測定すると、抵抗の2つの端点での電位差は異なる値を示します。これは、電圧計を使用して確認できます。

上で説明した状況から、標準的なオームの法則は次のように推測できます。

抵抗器の両端の電圧降下ERは、瞬時電流Iに比例し、次のように表すことができます。

ER = RI （式＃1）

上記の式では、 R は比例定数として定義され、抵抗の抵抗と呼ばれます。

ここで電圧を測定します IS ボルトでは、抵抗 R オームで、そして現在私アンペアで。

これは、単純な電気回路内の最も基本的な形でオームの法則を説明しています。
より複雑な回路では、コンデンサとインダクタの形でさらに2つの重要な要素が含まれています。

インダクタとは

インダクタは、電流の変化に対抗する要素として定義でき、機械システムの質量と同じように、電気の流れに慣性のような効果を生み出します。実験により、インダクタについて次のことがわかりました。

電圧降下 THE インダクタの両端は、電流Iの瞬間的な変化率に比例します。これは次のように表すことができます。

EL = L dl / dt （式＃2）

ここで、Lは比例定数になり、インダクタのインダクタンスと呼ばれ、で測定されます。 ヘンリー。 時間tは秒単位で与えられます。

コンデンサとは

コンデンサは、単に電気エネルギーを蓄える装置です。実験により、次の説明を得ることができます。

コンデンサ両端の電圧降下は、コンデンサの瞬間電荷Qに比例します。これは、次のように表すことができます。

EC = 1 / C x Q （式＃3）

ここで、Cは キャパシタンス 、およびで測定されます ファラッド 料金 Q クーロンで測定されます。

しかし以来 IC） = dQ / dt、 上記の方程式は次のように書くことができます。

現在の値 それ） 次の物理法則を適用して生成された方程式を解くことにより、特定の回路で解くことができます。

キルヒホッフの法則（KVL）を理解する

グスタフ・ロバート・キルヒホフ（1824-1887）はドイツの物理学者であり、彼の人気のある法則は以下のように理解されるかもしれません。

キルヒホッフの現行法（KCL）は、次のように述べています。

回路のどの時点でも、流入電流の合計は流出電流の合計に等しくなります。

キルヒホッフの電圧法則（KVL）は、次のように述べています。

閉ループ周辺のすべての瞬間的な電圧降下の代数的合計がゼロであるか、閉ループに印加される電圧が残りのループの電圧降下の合計に等しくなります。

例1： 以下のRLダイアグラムを参照し、式＃1,2とキルヒホッフの電圧を組み合わせることにより、次の式を導き出すことができます。

式：4

一定の起電力を持つこのケースAを考えてみましょう。

上記の式＃4で、E = E0 =定数の場合、次の式を駆動できます。

式：5

ここで、最後の項はゼロに近づきます。 t 無限に進む傾向があるので、 それ） 制限値E0 / Rになる傾向があります。十分に長い遅延の後、cの値に依存することなく、実質的に一定になります。これは、これが、私たちによって強制される可能性のある初期条件とは無関係であることも意味します。

初期条件をI（0）= 0とすると、次のようになります。