2進数システムのルーツは、中国文学にあります。現代のバイナリシステムは、1689年にゴットフリートライプニッツによって発明されました。彼の神学は、「何もないところからの創造」というキリスト教の考えに基づいていました。彼は、論理の口頭での発言を数学的な発言に変換できるシステムを見つけようとしていました。古典的な中国語の教科書「易経」で、彼は バイナリコード それは、人生を一連の単純な比率にまで減らすことができるという彼の理論を確認しました。次に、0と1の行の形式で情報を表すことができるシステムを作成しました。バイナリシステムの使用法は、16世紀以前の古代のテキストに記載されています。 1450年以前は、フランス領ポリネシアのマンガレバ島の住民がハイブリッド2進数10進数システムを使用していました。この記事では、2進化10進変換について説明します。
2進数システムとは何ですか?
2進数の使用法は、エジプト、中国、インドなどの古代文化のテキストに記載されています。このシステムでは、テキスト、データ、および数値は、2つの記号のみを使用する2進数として表されます。このシステムでは、数字は0と1の行として表されます。各桁は「ビット」と呼ばれます。 4ビットのコレクションは「ニブル」と呼ばれ、8ビットは「バイト」を形成します。
10進数システムとは何ですか?
10進数は、ヒンドゥーアラビア数字とも呼ばれます。これは位取り記数法です。数値を表すために10個の記号を使用するため、10進数システムとも呼ばれます。このシステムでは、記号0、1、2、3、4、5、6、7、8、および9が使用されます。シンボル「0」はインドで発明され、そのアイデアは貿易中にアラビア人によって東に伝えられました。したがって、このシステムは一般にヒンドゥーアラビア記数法として知られています。西洋文化におけるこのシステムの使用は、12世紀に商業と科学で始まりました。
2進数システムの使用
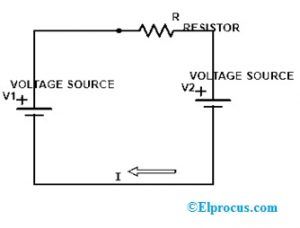
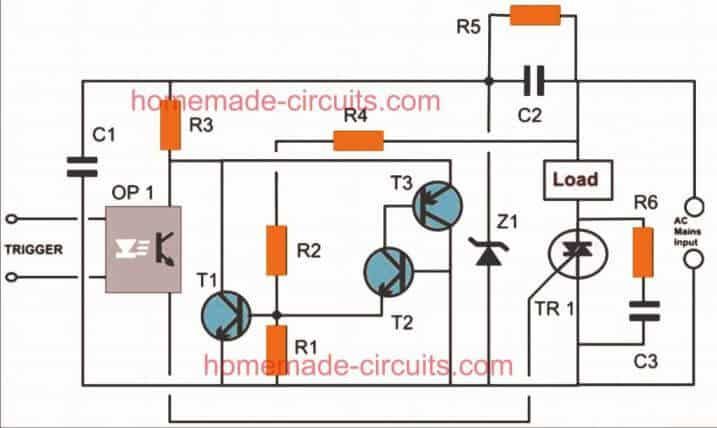
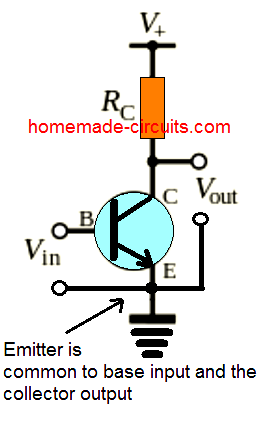
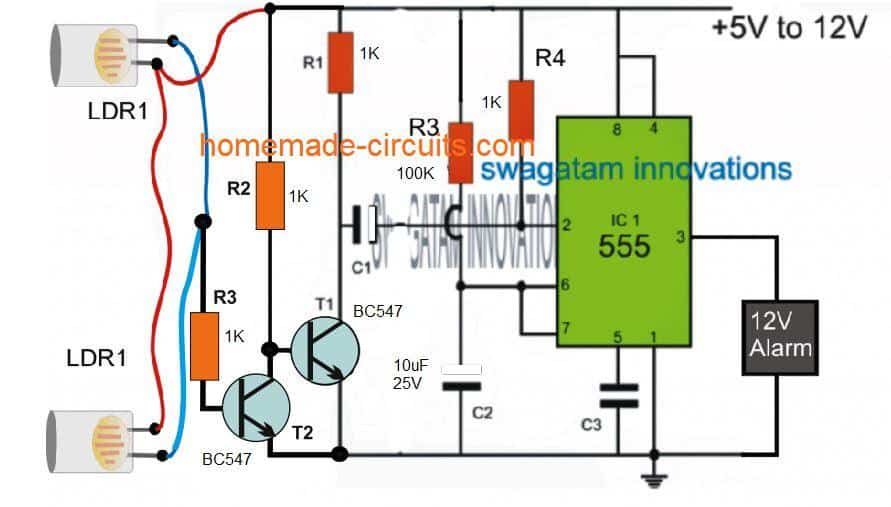
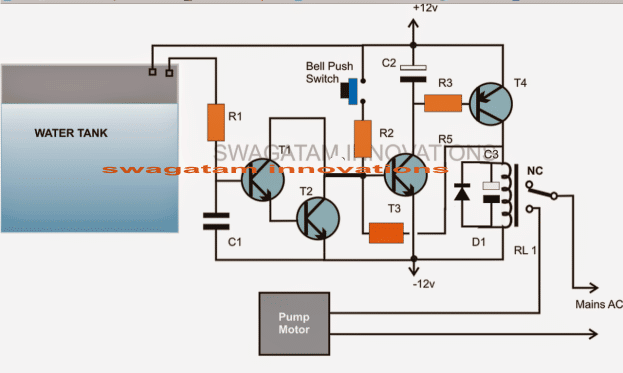
1847年、ジョージブールは、彼の論文「The Mathematical Analysis of Logic」で、ブール代数について説明しました。このシステムは、バイナリのON-OFFロジックに基づいていました。クロードシャノンは、ブール代数との論理の類似性に気づきました 電気回路 。 1937年、シャノンは彼の論文で彼の発見を発表しました。それは、バイナリシステムがデジタルロジック、コンピュータ、電気回路などで使用されている最初のポイントになりました…
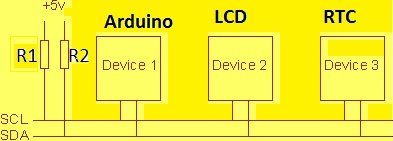
最近のすべてのコンピューターは、命令セットとデータストレージにバイナリエンコードを使用しています。デジタルデータはバイナリビットの形式で保存されます。デジタル 無線通信 バイナリビットの形式でデータを転送します。
10進数から2進数への変換方法
日常生活の計算やナンバリングには10進数を使用しています。しかし、コンピューターや電子機器などのマシンはバイナリを使用し、バイナリデータしか理解できません。したがって、10進数を2進数に変換することが重要です。
10進数を2進数に変換するには、数値を2で割ります。結果を以下に、余りを右側に記入します。余りがない場合は0を書き込みます。結果を2で割り、上記のプロセスを続行します。結果が「0」になるまで、このプロセスを繰り返します。余りをボトムアップで読み取ります。これにより、指定された10進数に相当する2進数が得られます。 MSBは最下位の剰余ですが、最初の剰余は2進数のLSBを形成します。
10進数から2進数への変換例
10進数から2進数への変換方法を理解するための例を見てみましょう。 10進数は基数10で表され、2進数は基数2で表されます。
2進数の右端のビットは最下位ビットと呼ばれ、左端のビットは最上位ビットと呼ばれます。

10進数から2進数への変換
上記の例では、10進数65の2進変換が示されています。上向きの矢印は、余りを書き留める順序を示しています。
2進化から10進への変換方法
10進数は、基数10の数値とも呼ばれます。これは位置番号付けシステムであるため、桁の桁の値を知る必要があります。右側から始めて、10進数システムの桁の値は10の累乗です。たとえば、1345の場合–桁の値5は10です。0.i.e。 1、場所の値4は10です1これは10位です。同様に、次の場所の値は100、1000などです…
したがって、指定された番号は次のようにデコードできます。
(1×1000)+(3×100)+(4×10)+(5×1)= 1345。
2進数システムも 位置番号付けシステム 。ここでは、底は2です。したがって、場所の値を見つけるために2の累乗が使用されます。したがって、2進数を10進数に変換するには、2進数に2の累乗を掛けて加算します。

Binary-To-Decimal-Conversion-Table
2進化から10進への変換例
変換を理解するために、例を見てみましょう。 1101を変換しましょう二10進数に。
LSBから始まり、1101二=(1×23)+(1×2二)+(0×21)+(1×20)
=(1×8)+(1×4)+(0×2)+(1×1):
= 8 + 4 + 0 + 1:
= 1310
したがって、1101の10進表現は13です。
10進数から2進数へのエンコーダ
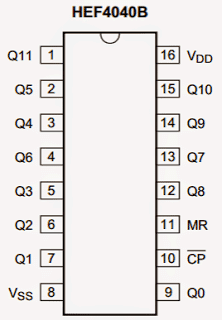
エンコーダー コンピュータシステムのコードコンバータとして使用されます。これらは、市場でICとして入手できます。 10進数を2進数に変換するには、Decimal toBCDエンコーダーを使用します。 BCDシステムでは、10進数は4桁の2進数として表されます。 0から9までの10進数をバイナリストリームに変換できます。
エンコーダーは 組み合わせ論理回路 。エンコーダーのリバースは、リバースアクションを実行するデコーダーです。 Decimal toBCDエンコーダの真理値表を以下に示します。

Decimal-To-Binary-Encoder-Truth-Table
上記の真理値表から、単語A3、A2、A1、A0の方程式を作成します。したがって、論理式は次のようになります-
A3 = 8 + 9:A2 = 4 + 5 + 6 + 7:A1 = 2 + 3 + 6 + 7:A0 = 1 + 3 + 5 + 7 + 9
ここで、上記の論理式を考慮して、ORゲートとの組み合わせ回路を形成します。

10進数から2進数へのエンコーダ
科学、通信、商取引の多くの分野で、デジタル技術がアナログ手法に取って代わりつつあります。さまざまな正確で手頃な価格の家電製品も増えています。これらのシステムはすべて、アルファベット、10進数、16進数など、さまざまな形式と表現で入力データを受け取ります。ただし、内部的にはすべてのデータが処理され、2進数とビットの形式で格納されます。したがって、コンピュータープログラマーおよび開発者にとって、これらのさまざまなタイプのデータすべてと2進数システムとの関係を知ることが重要です。 10進数45を同等の2進数に変換して、2進数変換についての理解を確認してください。